Our research focuses on cutting-edge exploration and cross-disciplinary applications of continuous-variable quantum computing frameworks, aiming to overcome performance limitations of classical computing in complex problem-solving. Key research priorities include advancing fundamental theories and algorithmic optimizations in continuous-variable quantum computing (e.g., efficient implementations of quantum search), constructing dynamic decision-making models for quantum reinforcement learning, developing high-dimensional information encoding and parallel acceleration techniques for quantum image processing, and innovatively designing duplication-free quantum neural networks to enhance resource efficiency. The overarching objective is to integrate quantum computational advantages with core demands in machine learning, image processing, and related fields, thereby establishing a scalable quantum intelligent algorithm framework. This initiative seeks to accelerate the practical deployment of quantum computing in optimization, artificial intelligence, and big data processing scenarios.

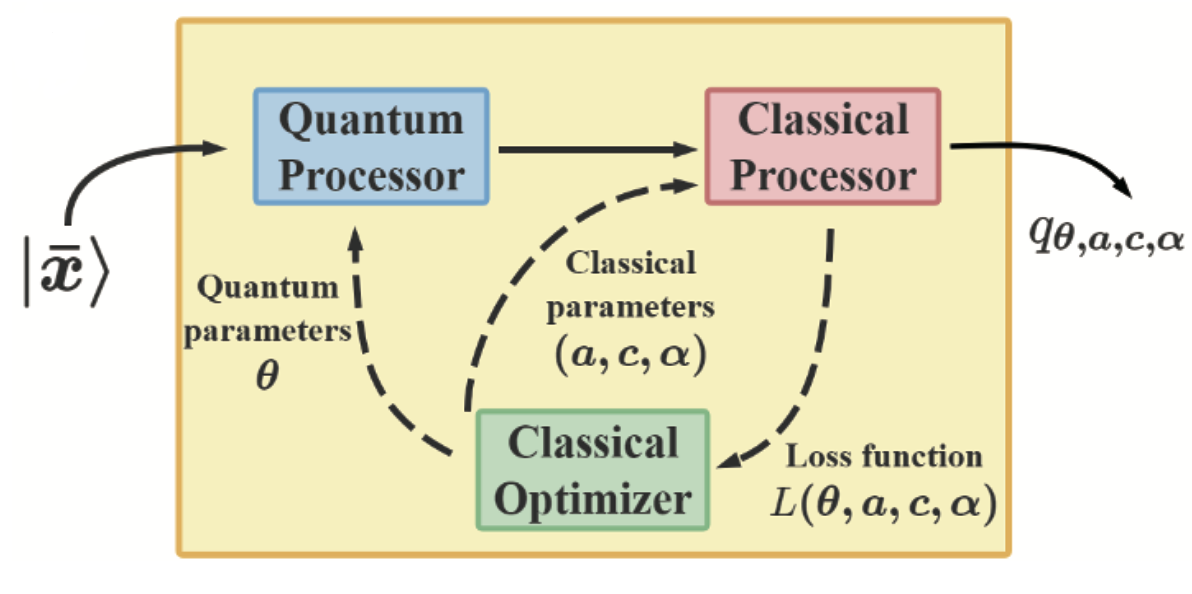
The duplication-free quantum neural network (DQNN) introduces nonlinearity by integrating a single quantum register with classical sigmoid functions, thereby eliminating the redundant designs in conventional quantum neural networks that rely on data duplication. This architecture employs multiple shallow variational quantum circuits and local observables for quantum state processing, coupled with classical nonlinear post-processing to achieve efficient learning, requiring only a logarithmic number of quantum bits $\log d$ relative to classical data dimensionality. Rigorously grounded in the universal approximation theorem under the $L^2$-norm framework, the model’s expressive power has been formally proven. Experimental evaluations demonstrate its superior performance with significantly lower relative errors in regression and classification tasks compared to QCL and CCQ benchmarks, exhibiting approximately 30% enhancement in noise robustness and achieving 97.6% classification accuracy. Practical validation through quantum phase transition identification (99.1% accuracy) further confirms its applicability. This resource-efficient and theoretically sound framework provides a viable solution for practical deployment on near-term quantum devices.

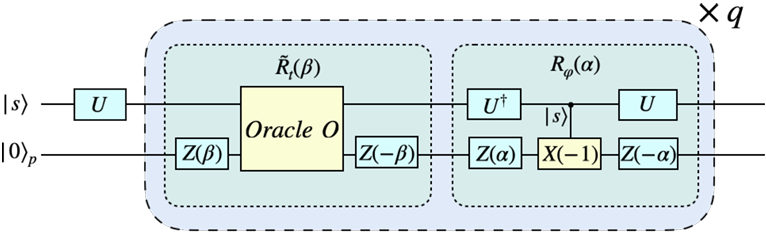
We propose a fixed-point quantum continuous search algorithm based on continuous-variable (CV) quantum computing to address continuous search problems (CSPs), demonstrating broad applicability in optimization, physics, and engineering domains. By designing a Grover iteration structure incorporating parameterized rotation operators, the algorithm achieves efficient search in continuous domains without discretization, while proving its optimal query complexity of $O(\frac{1}{\sqrt{\lambda}})$, where $\lambda$ denotes the measure ratio between the target solution space and the initial search space. The study further establishes a lower bound$\frac{1}{2\sqrt{2}}[(1+\sqrt{p}−\sqrt{1-p})\sqrt{n-2}]$ for the query complexity of arbitrary quantum algorithms solving CSPs, confirming the algorithm’s optimality. Additionally, we construct a quantum oracle framework tailored for continuous optimization, encoding gradient information into auxiliary quantum states via phase estimation techniques. Successful applications to non-convex optimization problems such as the Rosenbrock function and eigenvalue determination of continuous-spectrum operators highlight the algorithm’s advantages in convergence robustness and noise resistance. This work provides both a theoretical framework and practical implementation schemes for continuous-variable quantum computing in complex optimization challenges.

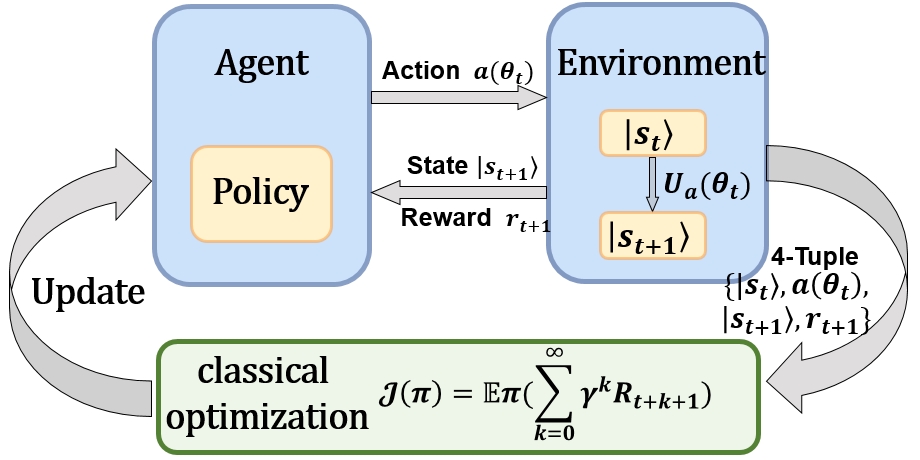
When applying reinforcement learning (RL) to quantum systems, significant challenges arise, particularly in addressing continuous action spaces where actions are not confined to discrete finite sets but span a continuous spectrum, leading to an exponential increase in computational complexity. This study proposes a quantum Deep Deterministic Policy Gradient (DDPG) algorithm tailored for continuous action spaces. The method employs variational quantum circuits to construct quantum neural networks, enabling the learning of optimal quantum operation sequences (i.e., control pulses) required to drive a quantum system from arbitrary initial states to target states. A key innovation lies in the algorithm’s ability to generate adaptive control sequences for any target state after a single training phase, eliminating the need for retraining when new target states are specified. The effectiveness of this approach is validated through numerical simulations on both single-qubit and two-qubit systems, and its application is further extended to solving quantum eigenvalue problems—fundamental challenges central to understanding the intrinsic properties of quantum systems.

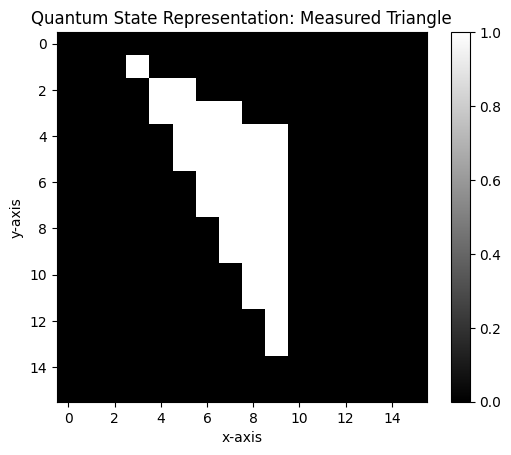
Quantum image states, a representation method encoding classical image information into quantum states, leverage the principles of quantum superposition and entanglement to significantly reduce image storage requirements and enhance processing efficiency. However, challenges persist in efficiently preparing such quantum image states. The primary objective of this study is to develop an efficient encoding scheme for mapping classical image information into quantum states while investigating optimization strategies for quantum circuits to improve preparation efficiency. To achieve this, we explore diverse quantum state preparation methodologies, analyze their performance metrics including circuit depth and gate operation complexity, and optimize quantum circuits by reducing redundant quantum gate operations to minimize resource consumption. Furthermore, we examine the correlation between the structural features of images and the ease of quantum state preparation, aiming to identify image characteristics that facilitate efficient quantum mapping. This investigation seeks to establish cost-reduction optimization schemes and ultimately develop a highly efficient quantum image state preparation framework.